Enem 2020 - Segundo dia Caderno Amarelo - Aplicação Regular

Um hotel de 3 andares está sendo construído. Cada andar terá 100 quartos. Os quartos serão numerados de 100 a 399 e cada um terá seu número afixado à porta. Cada número será composto por peças individuais, cada uma simbolizando um único algarismo.

Qual a quantidade mínima de peças, simbolizando o algarismo 2, necessárias para identificar o número de todos os quartos?

O fenômeno das manifestações populares de massa traz à discussão como estimar o número de pessoas presentes nesse tipo de evento. Uma metodologia usada é: no momento do ápice do evento, é feita uma foto aérea da via pública principal na área ocupada, bem como das vias afluentes que apresentem aglomerações de pessoas que acessam a via principal. A foto é sobreposta por um mapa virtual das vias, ambos na mesma escala, fazendo-se um esboço geométrico da situação. Em seguida, subdivide-se o espaço total em trechos, quantificando a densidade, da seguinte forma:

• 4 pessoas por metro quadrado, se elas estiverem andando em uma mesma direção; 
• 5 pessoas por metro quadrado, se elas estiverem se movimentando sem deixar o local; 
• 6 pessoas por metro quadrado, se elas estiverem paradas. 

É feito, então, o cálculo do total de pessoas, considerando os diversos trechos, e desconta-se daí 1 000 pessoas para cada carro de som fotografado.

Com essa metodologia, procederam-se aos cálculos para estimar o número de participantes na manifestação cujo esboço geométrico é dado na figura. Há três trechos na via principal: MN, NO e OP, e um trecho numa via afluente da principal: QR .

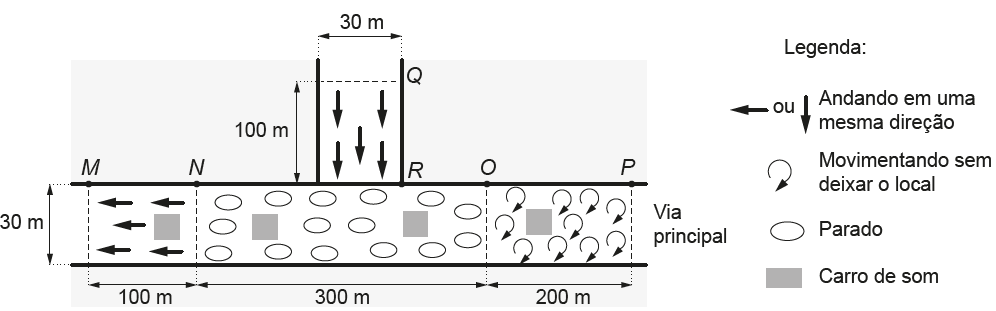
Obs.: a figura não está em escala (considere as medidas dadas).

Segundo a metodologia descrita, o número estimado de pessoas presentes a essa manifestação foi igual a

A Pesquisa Nacional por Amostra de Domicílios (Pnad) é uma pesquisa feita anualmente pelo IBGE, exceto nos anos em que há Censo. Em um ano, foram entrevistados 363 mil jovens para fazer um levantamento sobre suas atividades profissionais e/ou acadêmicas. Os resultados da pesquisa estão indicados no gráfico.

Jovens em atividade entre 15 e 29 anos (%)

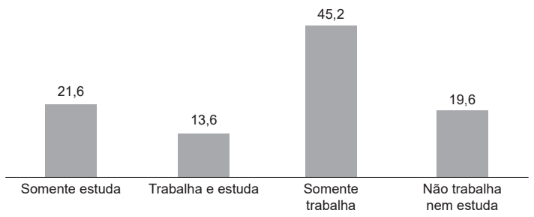
Disponível em: http://noticias.uol.com.br. Acesso em: 20 ago. 2014.

De acordo com as informações dadas, o número de jovens entrevistados que trabalha é

A Lei de Zipf, batizada com o nome do linguista americano George Zipf, é uma lei empírica que relaciona a frequência (f) de uma palavra em um dado texto com o seu ranking (r). Ela é dada por

$f = \cfrac {A}{r^B}$

O ranking da palavra é a sua posição ao ordenar as palavras por ordem de frequência. Ou seja, r = 1 para a palavra mais frequente, r = 2 para a segunda palavra mais frequente e assim sucessivamente, A e B são constantes positivas.

Disponível em: http://klein.sbm.org.br. Acesso em: 12 ago. 2020 (adaptado).    

Com base nos valores de X = log (r) e Y = log (f), é possível estimar valores para A e B.

No caso hipotético em que a lei é verificada exatamente, a relação entre Y e X é

Enquanto um ser está vivo, a quantidade de carbono 14 nele existente não se altera. Quando ele morre, essa quantidade vai diminuindo. Sabe-se que a meia-vida do carbono 14 é de 5 730 anos, ou seja, num fóssil de um organismo que morreu há 5 730 anos haverá metade do carbono 14 que existia quando ele estava vivo. Assim, cientistas e arqueólogos usam a seguinte fórmula para saber a idade de um fóssil encontrado: $Q(t) = Q_0 \cdot 2^{ - \cfrac{t}{5730} }$ em que t é o tempo, medido em ano, Q(t) é a quantidade de carbono 14 medida no instante t e Q₀ é a quantidade de carbono 14 no ser vivo correspondente. 

Um grupo de arqueólogos, numa de suas expedições, encontrou 5 fósseis de espécies conhecidas e mediram a quantidade de carbono 14 neles existente. Na tabela temos esses valores juntamente com a quantidade de carbono 14 nas referidas espécies vivas.

O fóssil mais antigo encontrado nessa expedição foi